A+B (MC) 공부법으로 불대수 입문을 쟁취하자

1월 2일에 A+B (MC) 문제의 풀테를 풀었습니다. 에디토리얼을 참고해 만점 풀이 방법을 알아봅시다. 이 글은 A+B (MC) 문제의 해답을 포함하므로, 문제를 직접 풀어보고자 하시는 분은 이론적 배경 정도만 읽으시면 될 것 같습니다..?

이론적 배경

• 이진수 가산기를 만들고자 할 때, 각 자릿수는 더하는 두 수의 자릿수와 바로 아랫자리의 받아올림값 3개의 수를 XOR한 것이 됩니다.
• 즉, A+B=C에서 A의 n째 자릿수를 x, B를 y, C를 z, A와 B의 n-1째 자릿수 받아올림을 w라 하면 (이때 x,y,z,w는 모두 0 혹은 1) z=x^y^w입니다.
• 어떤 자릿수에서 받아올림이 일어나는지는 세 비트 중 두 개 이상이 1인지 판단하여 알 수 있습니다.
• 즉, A의 n째 자릿수를 x, B를 y, A와 B의 n-1째 자릿수 받아올림을 w, n째 받아올림을 z’라 하면 z’=(x&y)|(y&w)|(w&x)입니다.
• 이것을 잘 구현하면 됩니다.

마인크래프트 최적화

• 만점 풀이를 위해, 우리는 이것을 비교기 없이 15틱 안에 계산하고 싶습니다.
• 이를 위해서는, 중계기의 lock 기능을 사용해야 합니다. 중계기의 옆으로 중계기로 신호를 주면, 중계기가 ‘잠금 상태’가 됩니다. 잠금 상태인 동안은(즉 신호를 받고 있는 동안은) 중계기에 신호를 공급하거나 끊어도 그 전의 출력값을 유지합니다. 대충 해보면 이렇습니다.
• 이건 사실 중요한 내용이 아닙니다. 중요한 것은, 만약 중계기의 입력 신호와 lock 신호를 동시에 넣으면 출력이 되지 않는다는 것입니다! 즉, 중계기의 입력 신호를 A, lock 신호를 B라 하면 이를 이용해 A & (~B)라는 연산을 최소 2틱만에 할 수 있습니다.
  • 여기서 ‘동시’라는 표현이 헷갈릴 수 있는데, lock 기능을 중계기로 주기 때문입니다. ‘동시’는 lock 신호를 담당하는 중계기에서 신호가 ‘빠져나오는’ 시점과 입력 신호가 같은 틱에 주어짐을 의미합니다. 따라서 원래 중계기와 lock 신호를 담당하는 중계기가 최소 1틱을 소요하기 때문에 위 연산의 소요시간은 2틱입니다.
  • 신호를 ‘동시’에 넣어야 한다는 것은 매우 중요한 조건입니다! 동시에 넣거나 lock 신호를 먼저 줄 수 있는데, 계산의 편의를 위해 이 글에서는 신호를 동시에 넣는 회로를 구현합니다.
• 이제 z=x^y^w와 z’=(x&y)|(y&w)|(w&x)를 구현하면 됩니다.
• 이때 주의할 것이 있다면, or 연산은 두 레드스톤 신호를 연결하면 얻을 수 있으나 이는 합선을 초래할 수 있습니다. 방향성을 강제하기 위해 중계기를 사용할 수 있지만 이는 1틱을 추가로 요구합니다.
• 그리고 생각할 것도 하나 추가하면, 어차피 시간을 잡아먹는 것은 받아올림입니다. 1의 자리에서 계산한 것을 받아올림해서 윗 자릿수로 전달하는 동안에는 그 위에서는 아무 것도 할 수 없습니다. 다시 말하면, 1의 자리를 제외하면 A나 B를 임의로 전처리해도 시간이 잡아먹히지 않습니다. 회로의 계산 시간은, (2개 비트 받아올림 연산) + 3 * (3개 비트 받아올림 연산) 이 됩니다.

식 구성

• 앞에서 설명한 A&~B 연산을 A?B라 작성합시다.
• A^B=(A?B)|(B?A)입니다. 즉 xor 연산은 2틱입니다.

  1의 자리 계산하기

• 현재 자릿수는 A^B, 받아올림은 A&B입니다.
• A^B는 2틱에 계산할 수 있습니다.
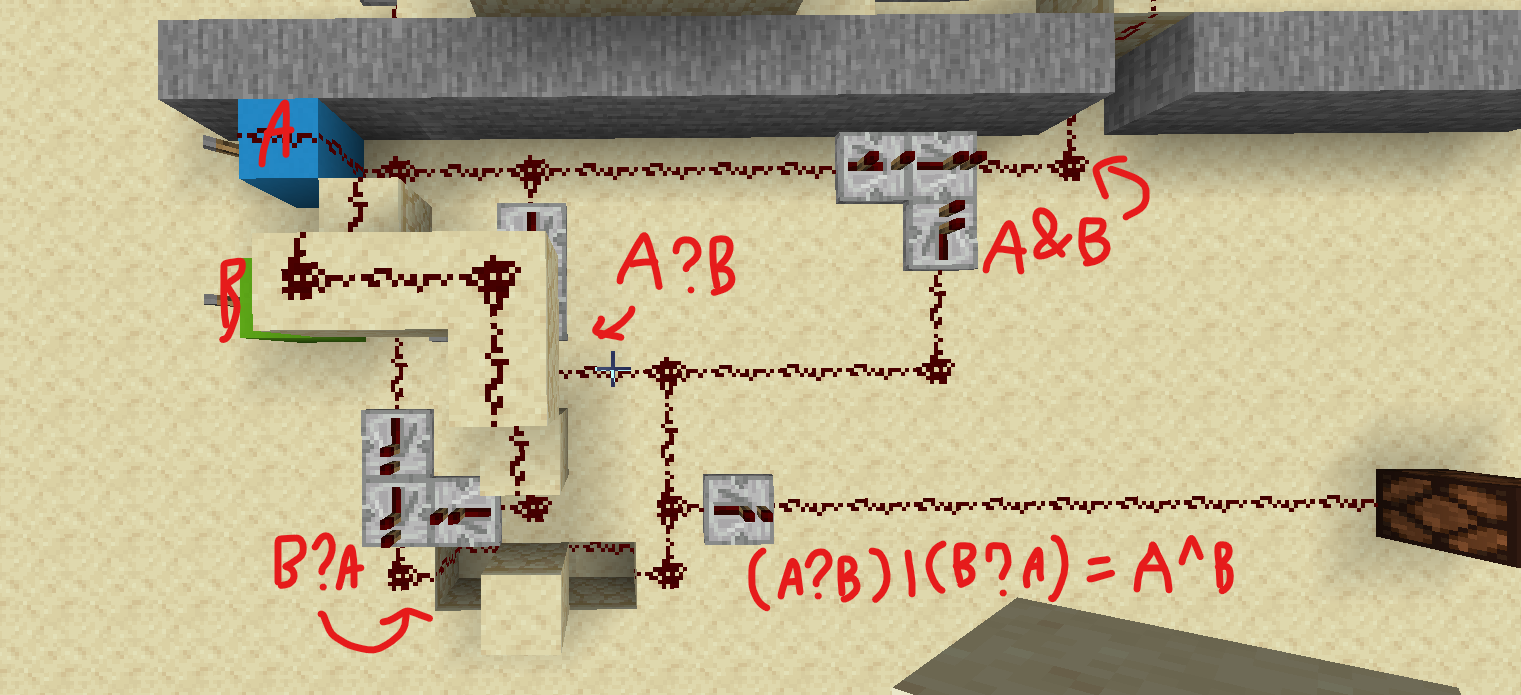
• A & B = A & ~(A|B ? B) = A & ~(A ? B) = A?(A?B)입니다. 이는 4틱입니다. 이렇게 짤 수 있습니다. 첫 번째 ‘?’ 연산이 2틱만큼의 딜레이를 만들기 때문에, 이에 맞게 두 번째 ‘?’ 연산의 입력 신호가 2틱 지연되어 있음을 확인할 수 있습니다. 이를 적용하지 않으면 A=1일 때 B와 상관없이 1이 출력됩니다.
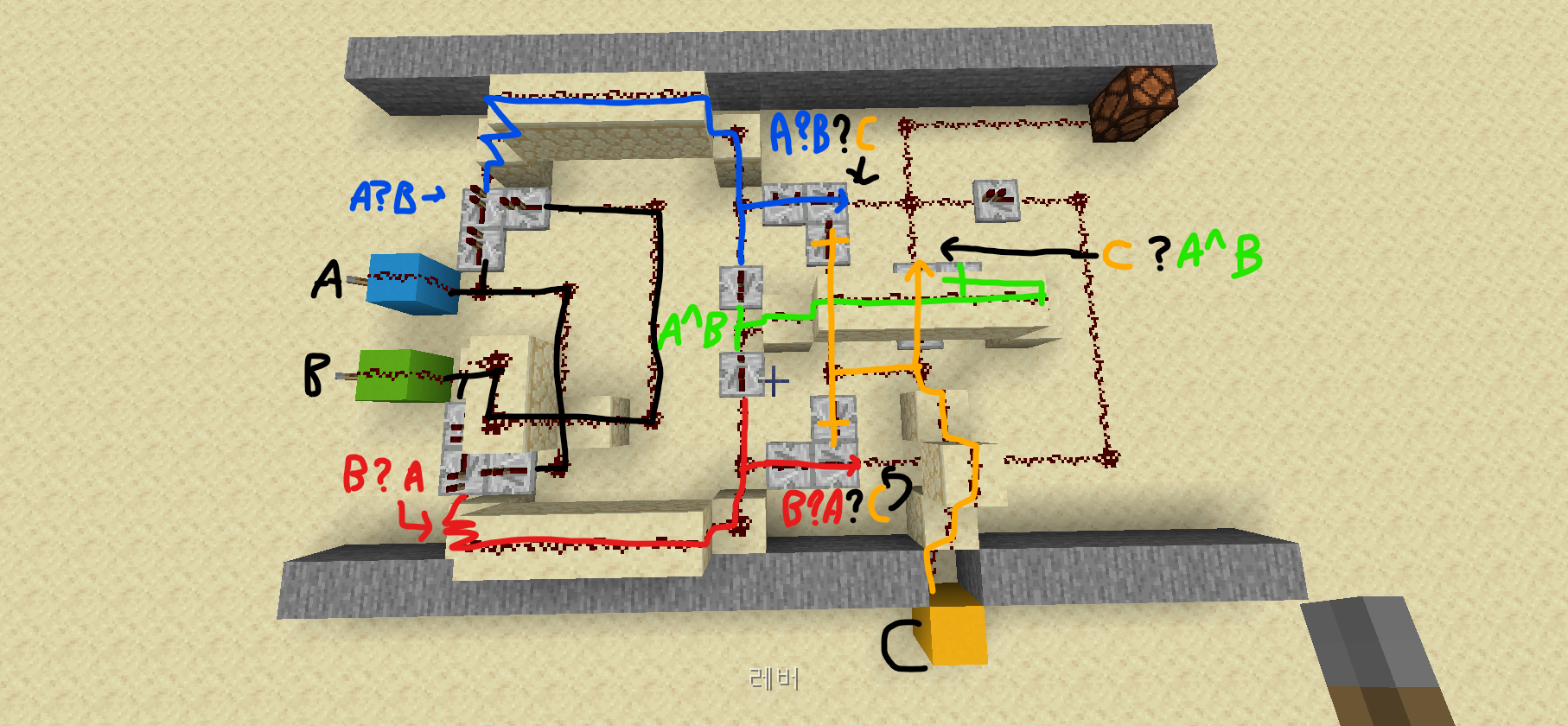
• 그렇다면 1의 자리의 전체 회로는 이렇게 구성할 수 있습니다. 이때, A?(A^B) = A?(A?B | B?A) = A?(A?B) | A?(B?A) 이고 이 역시 & 연산입니다. 따라서 위와 같이 회로를 짜도 됩니다. 그림(?)은 마우스로 그렸습니다. 잘 그렸죠?

  현재 자리 계산하기

• A^B^C를 빠르게 계산해 봅시다. A^B^C=1이려면…
  • C=0이고 A^B=1이거나
    • 즉 A=0, B=1, C=0이거나
    • A=1, B=0, C=0이거나
  • C=1이고 A^B=0입니다.
• 이를 ?와 or만으로 나타내면, ((A?B)?C) | ((B?A)?C) | (C?(A?B|B?A)) 입니다.
• 앞에서 설명했듯이, C가 오기 전까지는 A와 B를 전처리할 수 있습니다. 그렇다면 우리가 행해야 하는 연산은
  • X?C | Y?C | C?Z
• 의 형태가 됩니다. 따라서 2틱 안에 계산할 수 있습니다. 이런 식으로 짜면 됩니다. 레드스톤 신호는 입력이나 중계기로부터 15블럭 이내로만 전달되므로 조심해야 합니다.

  받아올림 보내주기

• (x&y)|(y&w)|(w&x)를 빠르게 계산해 봅시다. (x&y)|(y&w)|(w&x)=1이라면…
  • A&B=1이거나
  • A|B=1이고 동시에 C=1입니다.
• 따라서 A|B=1은 무조건 만족힙니다. A|B=1일 때 (x&y)|(y&w)|(w&x)=1이기 위해서는…
  • A^B=0이거나 C=1이면 됩니다.
  • 즉 (A^B & ~C)이지만 않으면 됩니다.
• 따라서 이를 ?와 or로만 나타낼 수 있게 됩니다. (A|B) ? ((A?B|B?A) ? C) 입니다.
• 전처리를 거치면, 우리가 행해야 하는 연산은
  • X?(Y?C)
• 의 형태가 됩니다. 그러나 이는 4틱입니다! 4*3+4=16은 15를 초과하기 때문에 마지막 테스트케이스를 맞을 수 없습니다.

  Joint Optimization

• 더 나아가기 위해서는 ? 연산에 대해 잘 생각해봐야 합니다. 결국 ? 연산이 2틱이나 걸리는 이유는 lock 신호가 중계기로만 전달되기 때문에 전달되는 데 1틱이 더 걸리기 때문입니다.
• 그런데, ? 연산의 출력은 중계기에서 바로 나옵니다. 그렇다면, (Y?C) 연산의 출력 중계기를 X?() 연산의 lock 입력으로 붙여버리면? X?(Y?C) 연산이 3틱 안에 해결 가능하게 됩니다!
• 사실 이걸 이용하면 일의 자리 연산도 3틱 안에 처리할 수 있습니다. 이건 직접 짜보시기 바랍니다(라기에는 그냥 3비트 가산기의 자리올림을 항상 0으로 두면 같은 기능을 하기는 합니다). 결론적으로 우리의 회로는 12틱 안에 계산을 끝마칠 수 있게 됩니다.

대충 이런 느낌으로다가 하면 됩니다. 간단해졌죠?

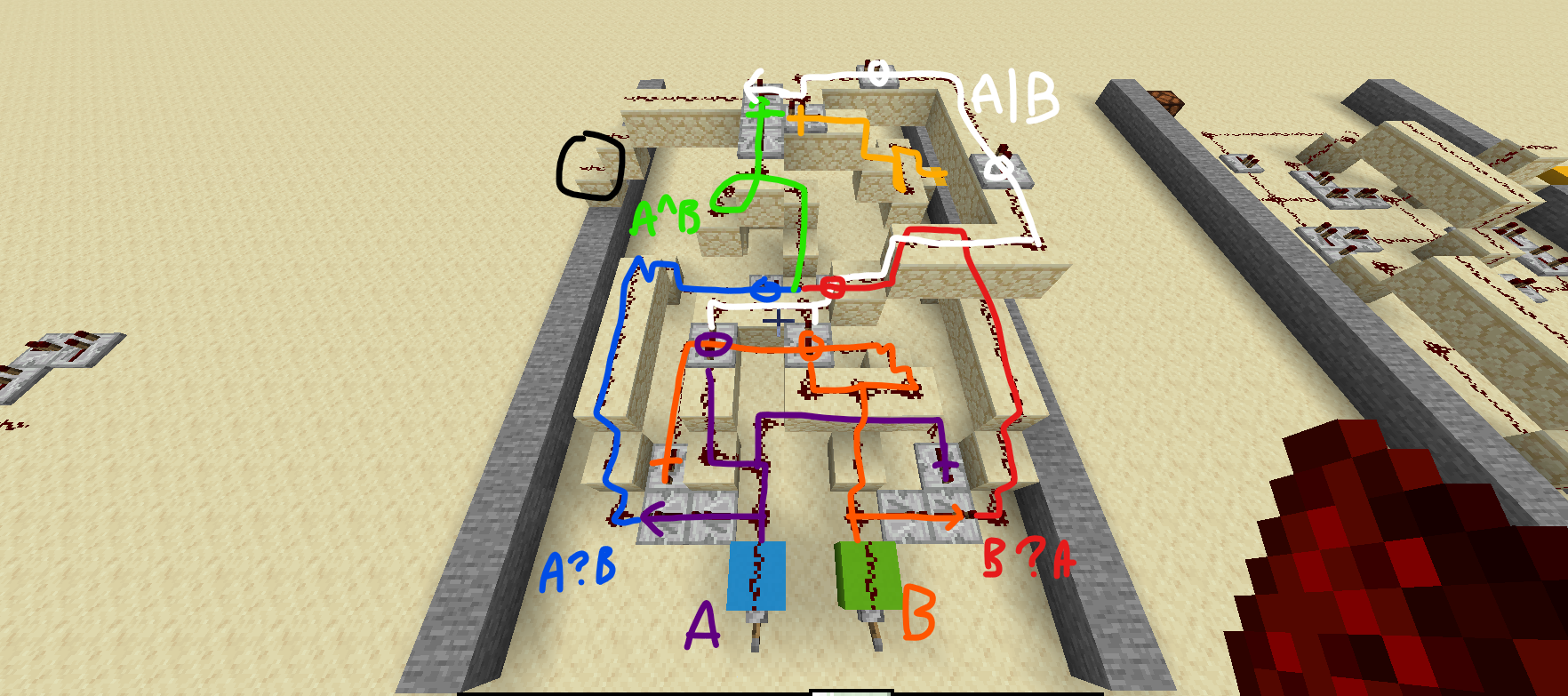조금 복잡해져서, ‘?’ 연산이 아닌 중계기를 다 동그라미 표시했습니다. 검은 동그라미가 출력입니다. 초록색, 노란색, 흰색이 만나는 곳이 X?(Y?C) 연산입니다.

• 현재 자리 계산 모듈 위에 받아올림 계산 모듈을 이어붙이면 됩니다.
• 받아올림 신호는 자릿수별로 4, 7, 10틱 째에 올라옵니다. 그에 맞춰 A|B와 A^B 신호를 딜레이해줘야 합니다. 저는 A?B와 B?A의 계산을 2틱에서 5, 8틱으로 바꾸고 A|B 전달 경로에 중계기를 추가로 다는 것으로 해결했습니다.

후기와 다양한 다른 방법

• 이정도면 간단하게 짠 것 같습니다.
• 굳이 할려면 이런 식으로 Joint Opt의 이점을 최대한 가져갈 수 있겠으나, 굳이 이렇게까지 해야 하나 싶네요. 나중에 틱을 더 적게 쓰는 문제가 나오면 사용해보도록 하겠습니다.
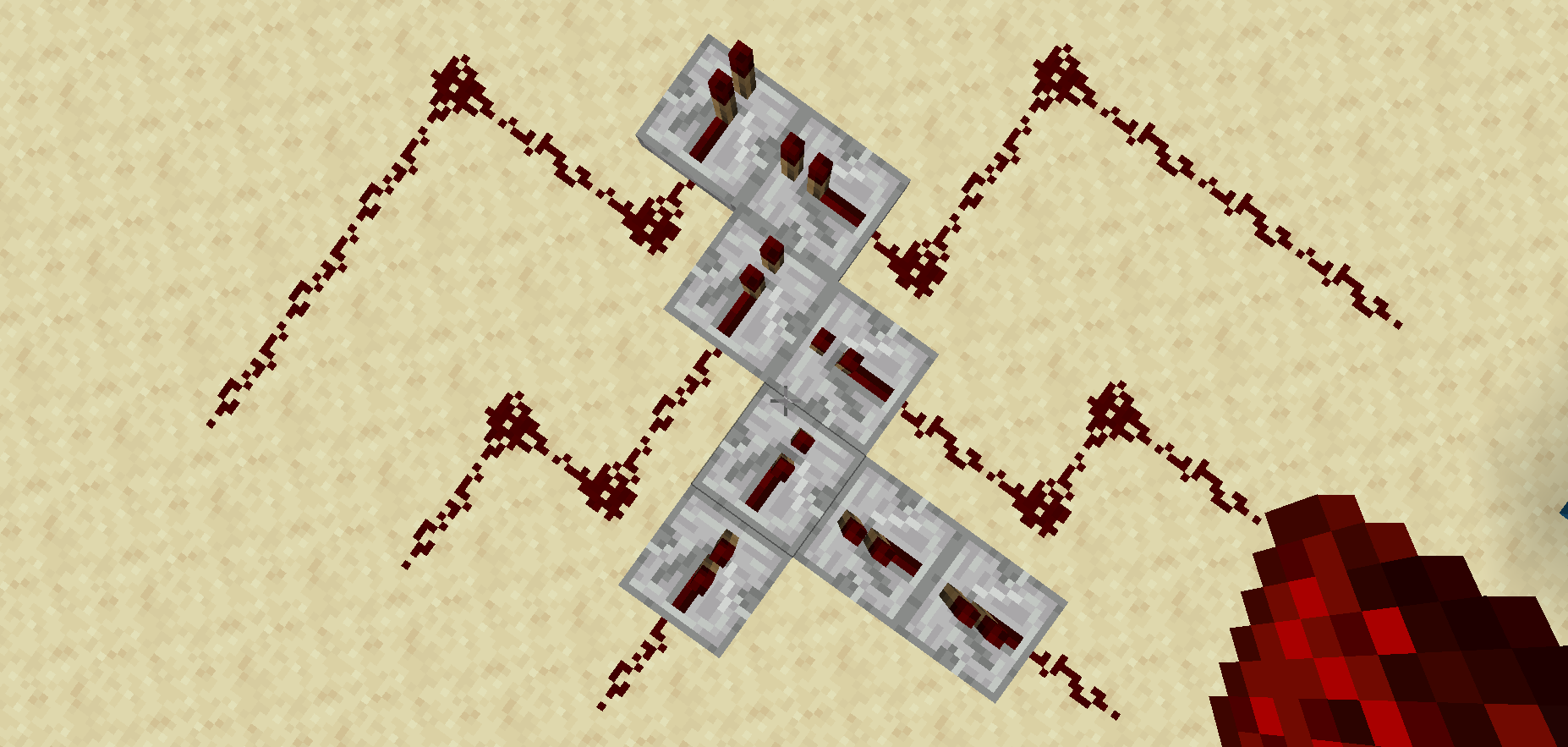
• Joint Opt는 사실 1의 자리에서도 쓸 수 있습니다. 이 경우 3+4*3=15틱이므로 나머지 층에서 Joint Opt를 사용하지 않아도 아슬아슬하게 코드가 돌아갑니다.
• or 연산의 방향성을 고정하는 작업을 할 때, 회로의 길이를 길게 빠는 것도 방법입니다. 서로를 향해가는 거리는 15 초과, 각각에서 출력으로 가는 거리는 15 이하로 잡으면 할 수 있기는 합니다.